Algoritmos de Grafos: Dijkstra, Kruskal y Prim

Descripción:

El algoritmo de Dijkstra es utilizado para encontrar el camino más corto desde un nodo de origen a todos los demás nodos en un grafo con pesos no negativos.

Detalles:

• Inicializa la distancia del nodo de origen a 0 y la de los demás nodos a infinito.
• Usa una cola de prioridad para seleccionar el nodo con la menor distancia conocida.
• Para el nodo seleccionado, actualiza las distancias de sus vecinos si se encuentra un camino más corto.
• Repite hasta que todos los nodos hayan sido procesados.

Ejemplo de uso:

• Redes de rutas (encontrar el camino más corto entre ciudades).
• Sistemas de navegación GPS.
• Redes de computadoras (rutas óptimas para la transmisión de datos).

Descripción:

El algoritmo de Kruskal es utilizado para encontrar el Árbol de Expansión Mínima (MST, por sus siglas en inglés) en un grafo, lo que minimiza el coste total de conectar todos los nodos.

Detalles:

• Ordena todas las aristas del grafo en orden ascendente según su peso.
• Inicializa un bosque (conjunto de árboles) donde cada nodo es un árbol separado.
• Itera sobre las aristas ordenadas y añade la arista al árbol si no forma un ciclo (usando la estructura de conjuntos disjuntos).
• Repite hasta que el árbol tenga (V-1) aristas (donde (V) es el número de nodos).

Ejemplo de uso:

• Diseño de redes eléctricas.
• Optimización de redes de comunicación.
• Construcción de carreteras para minimizar el coste total.

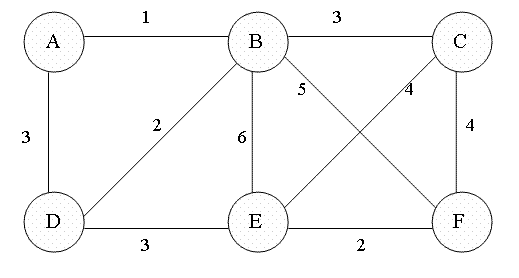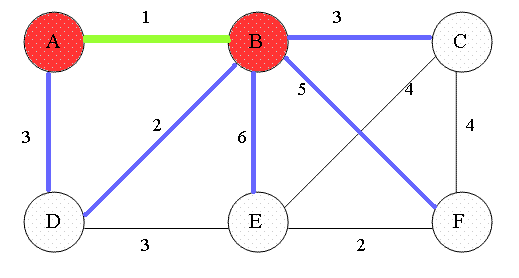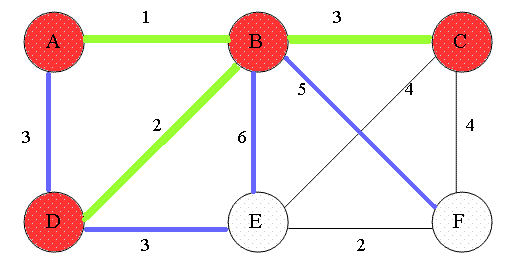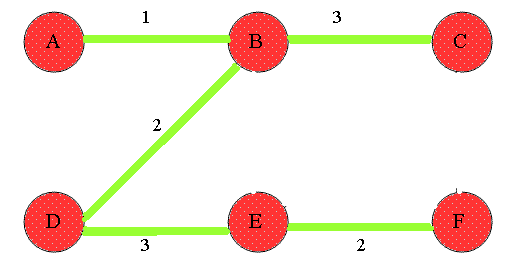
Descripción:

El algoritmo de Prim también se utiliza para encontrar el Árbol de Expansión Mínima de un grafo. A diferencia de Kruskal, este algoritmo expande el MST desde un nodo inicial.

Detalles:

• Inicializa el MST con un nodo inicial.
• Usa una cola de prioridad para seleccionar la arista de menor peso que conecta un nodo en el MST con un nodo fuera del MST.
• Añade la arista seleccionada al MST.
• Repite hasta que todos los nodos estén incluidos en el MST.

Ejemplo de uso:

• Diseño de redes de tuberías.
• Instalación de cables de fibra óptica.
• Sistemas de telefonía para minimizar el costo de infraestructura.

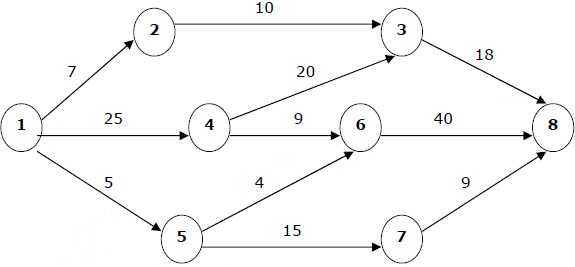
Descripción:

El algoritmo de Ford-Fulkerson se utiliza para encontrar el flujo máximo posible desde una fuente a un sumidero en una red de flujo, que es un grafo dirigido donde cada arista tiene una capacidad.

Detalles:

• Inicializa el flujo en todas las aristas a 0.
• Busca un camino aumentante desde la fuente al sumidero usando un algoritmo de búsqueda (como DFS o BFS), en el grafo residual.
• Determina la capacidad residual mínima a lo largo de este camino aumentante.
• Aumenta el flujo a lo largo del camino en la cantidad determinada en el paso anterior.
• Actualiza el grafo residual.
• Repite los pasos 2-5 hasta que no haya más caminos aumentantes.

Ejemplo de uso:

• Redes de transporte: Optimización del flujo de tráfico.
• Sistemas de telecomunicaciones: Maximización del flujo de datos a través de una red.
• Gestión de recursos hídricos: Maximización del flujo de agua a través de una red de tuberías.